Scylla and Charybdis

A fable of decision theory.

Emily Wilson is on Substack! In 2020, my spouse and I took turns reading her translation of The Odyssey aloud, beginning to end. Her version works well as a read-aloud, as any translation of an ancient epic should. It inspired me to write a story in a similar style (except no meter), which I then never published anywhere. But today I felt motivated to edit and illustrate it, so here you go.

---

Is everybody else as excited about the newly-discovered version of Homer’s Odyssey? I’m no poet, but I’ve been working on an amateur translation of one passage to get a sense of the differences. It’s a bit from where Odysseus tells the story of how the goddess Circe warned him about the dangers on his travels.

After she warned me of the dangers of the Sirens, I called in sailors to hear the rest.
I hoped that with their council we might avoid more disaster than with my wits alone.
In came Eurylochus, my cautious second, the only to avoid strange Circe’s traps.
I called in too Polites, my dearest friend, who ever urged me on to boldness.
In too came youthful Elpinor, a man of no great talent who was nearby.
Then patient Circe spoke again.

“Soon shall you come upon two cliffs, so close an arrow could be shot from one to one.
The way home lies on the water between. The cliff that faces west is home to monstrous Scylla.
She has six long-necked heads, each like a great wolf, and should you pass too near,
Each of those heads will claim the life of one of your crew. Such is the deadly hunger of Scylla.
Beneath the other cliff sits gods-cursed Charybdis, beneath a great tree bearing figs.
All day Charybdis drinks black seawater, then vomits it back up. This fate was given her.
A ship that passes near will be sucked in and destroyed. Such is the deadly thirst of Charybdis.”

Circe’s Riddle

I asked her then,
“Goddess, what must I do, what course must I set, to carry us safely between these cliffs?”
The lovely Circe then replied,
“There is no safety, and I cannot say what you must do, only of the consequences.
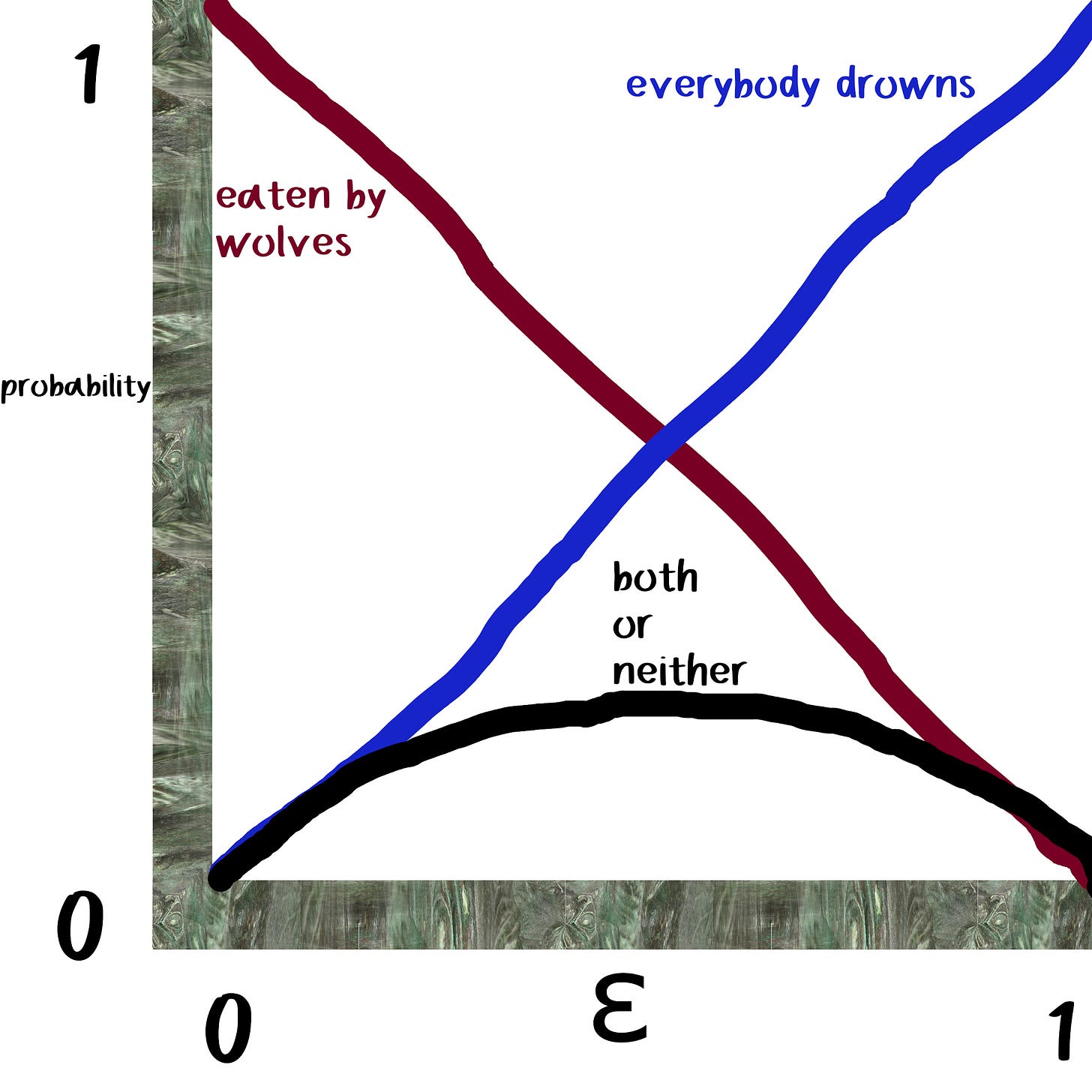
You may pick any number from 0 to 1, which we may call ε, and I will tell you of a course.
If you set that course, then with probability ε, implacable Charybdis will doom your ship.
And with probability 1-ε, vicious Scylla will devour six men aboard that vessel.”

Strange Circe had taught us much in our year on her enchanted isle.

This was not the first time she had tormented us with algebra.

I answered her wisely.

“Kindly Goddess, tell me. Are these probabilities disjoint or independent?
That is, will being eaten by wolf-like heads mean we are safe from whirlpools?”

Patient Circe then explained.

“Scylla’s necks are long and flexible, and the motion of water is complicated.
The probabilities are independent. You might avoid both monsters, one, or neither.
Now tell me what value you prefer for ε, and I will tell you of the course to set.”

Elpinor’s Guess

Elpinor spoke first, as men of no great talent often leap to instruct those of wisdom.
“Lovely woman, I have attended to these arts.
I can see that lower values of ε bring us toward the lesser danger,
And higher values bring us toward the greater.
It’s clear then that a value below one half will set us on the wiser course.
I would set ε to be one quarter, as that is very small.
We would be safe from Charybdis and might escape Scylla.”

Polites’s Analysis
Then spoke eager Polites, whom I had had to rescue from one of Circe’s traps,
And who, in his way, then rescued me from one of hers.
“Young Elpinor, you’ve chosen a number that sounds good to you.
But this is a grave matter and we must apply ourselves and math to it.
Our goal must be to maximize the chance that neither monster gets to claim our lives.
This probability may be given in terms of ε as the product of each probability of escape.
For the product of two independent probabilities gives the probability that they both occur.
We wish to maximize ε * (1 - ε). Elpinor’s value of one quarter would give three sixteenths.
Which is to say, in thirteen out of sixteen cases would we come to harm.
Our best odds come when ε equals one half. Then we will have one chance in four.
Call it four chances in sixteen, and now it’s clear this is superior to three.”
Elpinor’s tongue was still. He was too awed to speak against skilled Polites,
Who had deployed mathematics to argue his point.

I spoke up in his stead.

“Polites, your method treats the two harms as equal.
You ignore the greater danger posed by Charybdis, who would unknowing kill us all.
No wonder then you give an answer of one half, indifferent between the two.”

Polites, undeterred, replied to me.

“My King and Captain, I think it only right. Advice exists to warn us off from harm.
For Circe to give us an instruction that drives us toward a monster would not be good hospitality.
Any course but one straight down the middle would violate this law.”

Eurylochus Advises Caution, Sort Of

I turned then to careful Eurylochus, whose advice I often sought, and received more often yet.
Many times, while fleeing from a monster, had I wished I had listened to noble Eurylochus.
I spoke to him.

“Eurylochus, you have heard two numbers said. Please tell me, what value would you give?

Would you ask Circe for a course that gave one quarter, one half, or some other chance
Of sinking to the bottom of the wine-dark sea, our souls and treasure lost to cruel Poseidon.”

Eurylochus answered me.

“One.”

Elpinor fell off his chair in comical astonishment. Polites gave a haughty snort,
As when a dog, pacing in boredom, sees his master sit and protests his sloth.
Calm Circe alone did not react.

I spoke again to Eurylochus, demanding,

“Have you perhaps not understood the problem?
ε = 1 would doom us all, with certainty. Surely that cannot be what you want.”

Eurylochus spoke hoarsely, weeping.

“Cunning Odysseus, I must agree that if we say this number to this witch,
The course she gives will kill us all, and that if we give any other number we might be saved.
I’d dearly like to return home to sweet Ctimene whom we both love.
Yet still I answer ‘one’. 
When someone speaks to you of total stakes, of paths where all is gained or all is lost,
Then you must not believe them. Otherwise, you can be made to do anything.
Circe tells us that if we do not steer towards a vicious monster, a giantess whose fearsome jaws
We will be able clearly to behold atop the cliff, a whirlpool will appear from nowhere and sink us.
If we believe her, we are no better than a fool who gives his coin to a charlatan promising riches.
If we believe her, why not believe a rogue who tells us to do something truly mad,
Like reject Olympus’s gods and worship one alone, or else be tortured in the depths of Tartarus.
With high enough numbers, mathematics can make you do anything.
The only safety is to reject absurdity, no matter how compellingly expressed.”

Proud Circe then spoke scornfully.

“Mortal Eurylochus, how can you doubt my knowledge?
The seed has not yet been planted that will grow into the bush
Whose fruit will be carried by a bird across a sea
To grow in the spilled blood of the murdered hero who will found the kingdom of Persia.
Yet I have taught you the secrets of Persian sages, of algebra and algorithm.
You know that I see all, and you know I swore to handsome Odysseus that I would not lie.”

Forceful Eurylochus wiped away his tears and answered the Goddess’s challenge.

“Wise Circe, you have shown me things no mortal man or woman could.
I have full faith in the truth of what you tell us.
But so feels the fool ensorcelled by imaginary gold, who loses what gold he has.
So feels the cultist told to blaspheme the true gods out of fear of imaginary punishment,
And so offend them and bring on a life of misery.
I must answer in the way I would like all men like me to answer,
In accordance with the universal law.
I do not want all men to be so easily exploited, and so logic demands that I answer ‘one.’
Any other answer would imply a world where charlatans can manipulate even the most wise.”

While Eurylochus spoke, Circe drew from her robes a fig and ate it. When both were done, she spoke again.

“Cunning Odysseus, your men have each given a number, but you are the captain.

Only the number you say matters. Tell me your value for ε, and I will tell you your course.

Then we may move on to discuss the dangers of the island of Thrinacia.”

Odysseus’s Decision

I answered the Goddess.

“All-seeing Circe, you know already that I will answer with a mystical number,
Another secret you have taught us from the unborn Persian sages.
You know that I will answer ‘zero’, and choose the certain pain of losing six of us,
Rather than invite any risk of losing all.

But I owe it to my three councilors to give my reasoning.

Far-seeing Eurylochus is right. For the method that I use to be correct, it must remain correct
In aggregate, when applied by all who think as I think.
As Elpinor said, one must weigh the greater harm greater and the lesser less.
But to apply this principle correctly, I must use mathematics as knowledgeable Polites did.
If I were admiral of a fleet, I’d want the greatest number of my sailors to survive.
I’d order my captains to give orders thus.

If I ordered all my captains to give a probability of ε,
That proportion of my ships would sink, with all hands lost.
1-ε would lose six men to the horrible jaws of six-headed Scylla.
The total lost to Charybdis, assuming fifty to a ship, would be 50*ε,
While the total lost to Scylla would be (1-ε)*6, or indeed a bit less,
As sailors cannot die twice and ε*(1-ε)*6 would be double-counted.

So the formula I would minimize is 50*ε + (1-ε)*6 - ε*(1-ε)*6,
Were I an admiral, and so emerge with the greatest fighting force.

I am alas one captain of fifty sailors and one ship, the others lost.
But if I imagine an admiral giving me an order and obey it,
I am acting in accordance with a law that will prevent harm,
And from which any deviation would cost lives.

And so I multiply probabilities by costs, treating them the same as proportions.
A one-half chance of two deaths I count the same as a certain death of one.
If I put zero into my admiral’s formula, I’d end up with 6 deaths.
If I put one-quarter in, I’d get over 15.
One half would give over 26, and 1 would give the full 50.
I then choose zero, or near enough to zero as you will allow, Goddess,
As you did not say whether the interval was open or closed.”

Elpinor’s Objection

Elpinor had recovered from his fall, and spoke to me.
“Lord Odysseus, I trust you in all things. But please explain.
Your answer zero is the same as if Circe had not warned you of Scylla!
Surely a wise decision takes into account all known information.”

I gave him the explanation that he sought.

“Elpinor, accounting for all that is known is the way to appear wise.
But seeming and being are not always the same thing.
When making a decision using numbers, the sign of the numbers matters,
But the magnitude does not always do so.

If you offer me three gold coins for one, I will accept.
If you offer me three gold coins for two, my answer will not change,
despite the numbers shifting.
Decreasing ε decreases deaths. It does not matter by how much.”

Eurylochus Is Offended
Where Elpinor was meek, Eurylochus was angry. He rose from his chair and spoke harshly.
“You condemn six of us to death to avoid a far-fetched catastrophe,
One that we have never seen occur, while we have seen many of our number
Eaten by monsters. How can you trade what is known and clearly true
For what is absurd and merely prophesied?”

I replied tolerantly.

“Eurylochus, I am troubled by your argument, and cannot easily refute it.
But surely it could just as easily be made the other way?
A world in which none try to avoid a grandiose catastrophe
Is a world doomed, as soon as one eventually comes along.
If there is any chance that my line continues forever,
It comes only in a world where I and my descendants try to avert great disaster,
Even at immediate cost and the risk of being foolish.”

I thought I had persuaded him, but I had not, and disaster followed.