When you move your hand, every motion is controlled by some part of your nervous system, even if it’s a reflex. Birds flap their wings the same way—each flap is triggered by a separate electrical signal. But some muscles move on their own. Most flying insects can send one signal to turn their wings on, and another to turn them off, only assuming direct control when they need to steer.
The key difference here is that a fruit fly needs to flap its wings much more rapidly than a goose does. A goose can flap its wings four times in a second, if it’s really making an effort, while a fruit fly’s tiny, weaker wings need to flap about two hundred times a second to keep it airborne. A fruit fly doesn’t have time for a central control mechanism.
We humans have one muscle, that we know of, that works similarly. Our hearts, like most mammals’, are quasi-autonomous—if you get startled, say, and your heart rate increases, it’ll stay elevated for a bit even after your brain decides there’s no danger.
These two kinds of muscle designs are an example of a power vs. control tradeoff. To get sustained rapid motion out of a muscle, you need to give up some control.
This is not a metaphor it’s just a thing that happens in many different domains
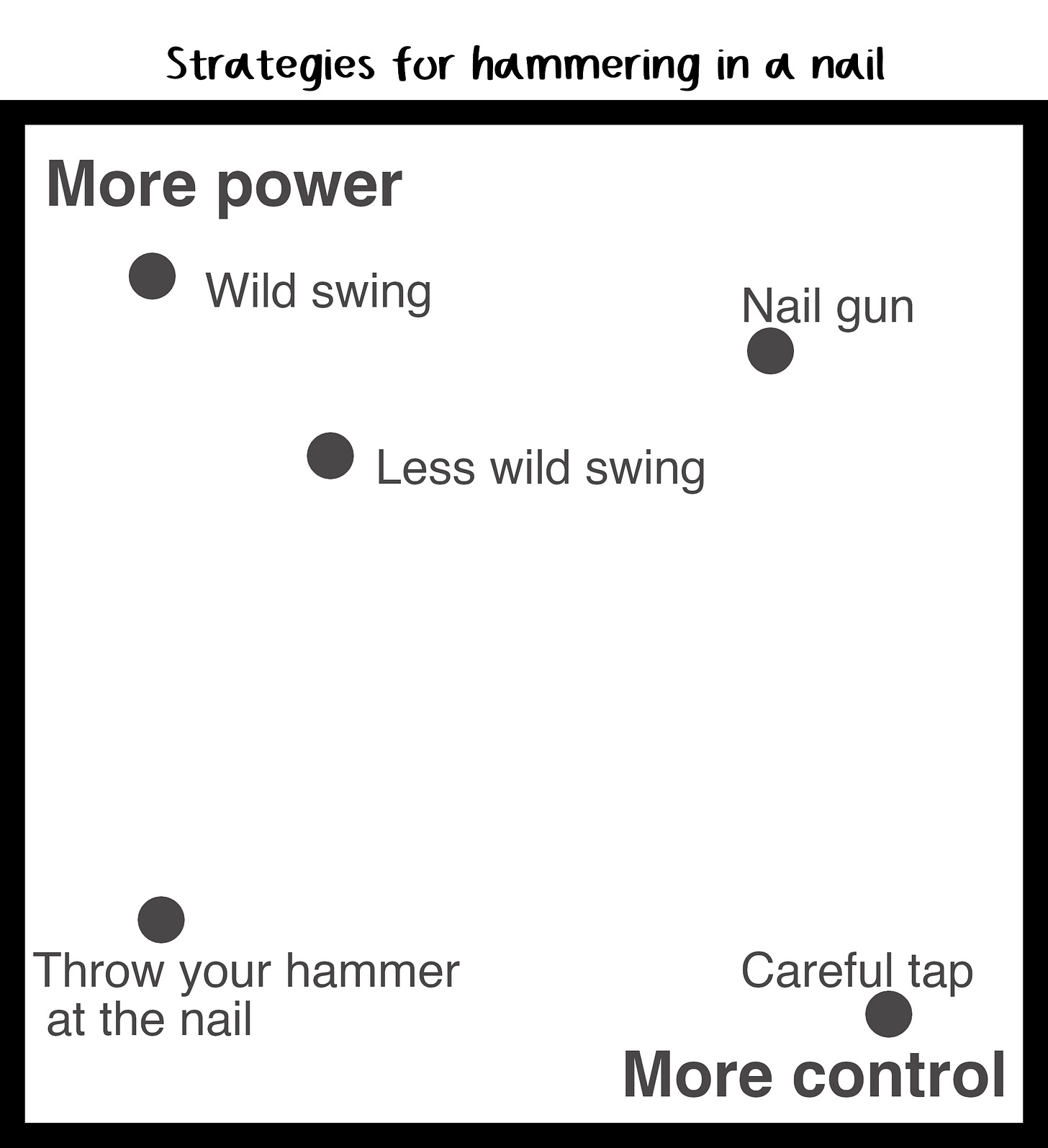
When you hold a hammer or a baseball bat right at the base, you get the full advantage of its length, allowing a powerful swing, but you might miss. “Choke up,” move your hands up to effectively make your lever shorter, and you gain precision but lose oomph.
Tennis players, in particular, talk about both swings and racket design in these terms. According to Busker Dan, it’s also the right way to think about singing with an unaided voice. It shows up in all sorts of engineering problems.
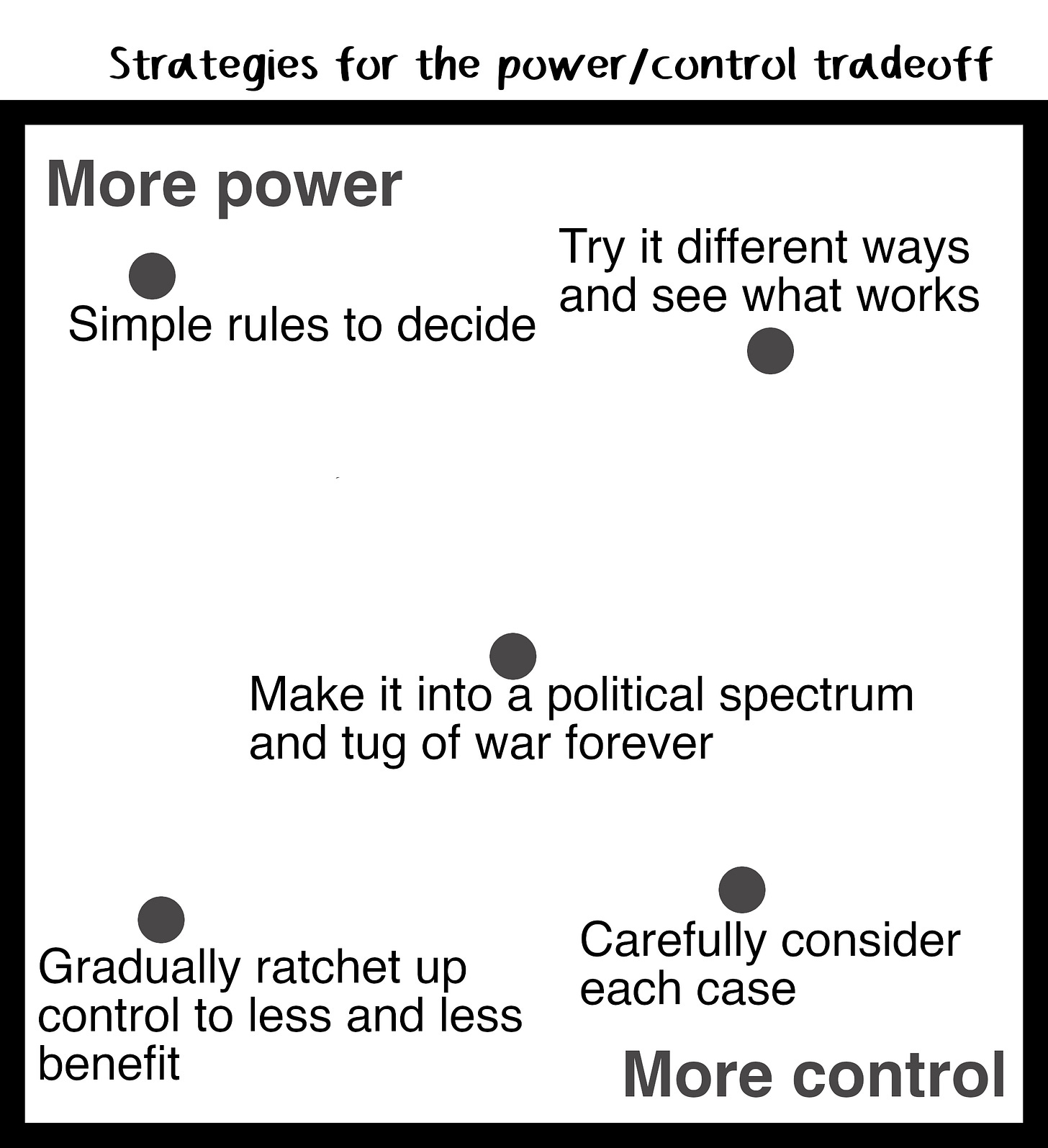
As with any kind of tradeoff, it’s important to remind yourself of two basic rules. One is that the right answer depends on the situation—the goose and the fruit fly are both making the evolutionarily optimal choice. The other is that it’s usually possible to break the rules—increase one without decreasing the other (hooray!) or decrease one without increasing the other (oh no!).
In Education
Students learn more, and retain more, when they’re interested in the subject. I don’t think I need a citation here. If you encourage or coerce someone to take a course they’re not interested in, they will learn less, in total. In exchange, you’ve exerted more control over what they learn. Which can be worth it! If everybody learned their rights as workers in school, we’d probably be better off. As it is, in most places, your employer is the one charged with this task, which is a wee bit of a conflict of interest. A day spent learning your rights is likely to be more valuable as a teenager than a day spent doing whatever you want, even though you’ll learn less.
We don’t make this decision mindfully enough as a society. In a little over a century, we’ve managed to sleepwalk into a corner.1
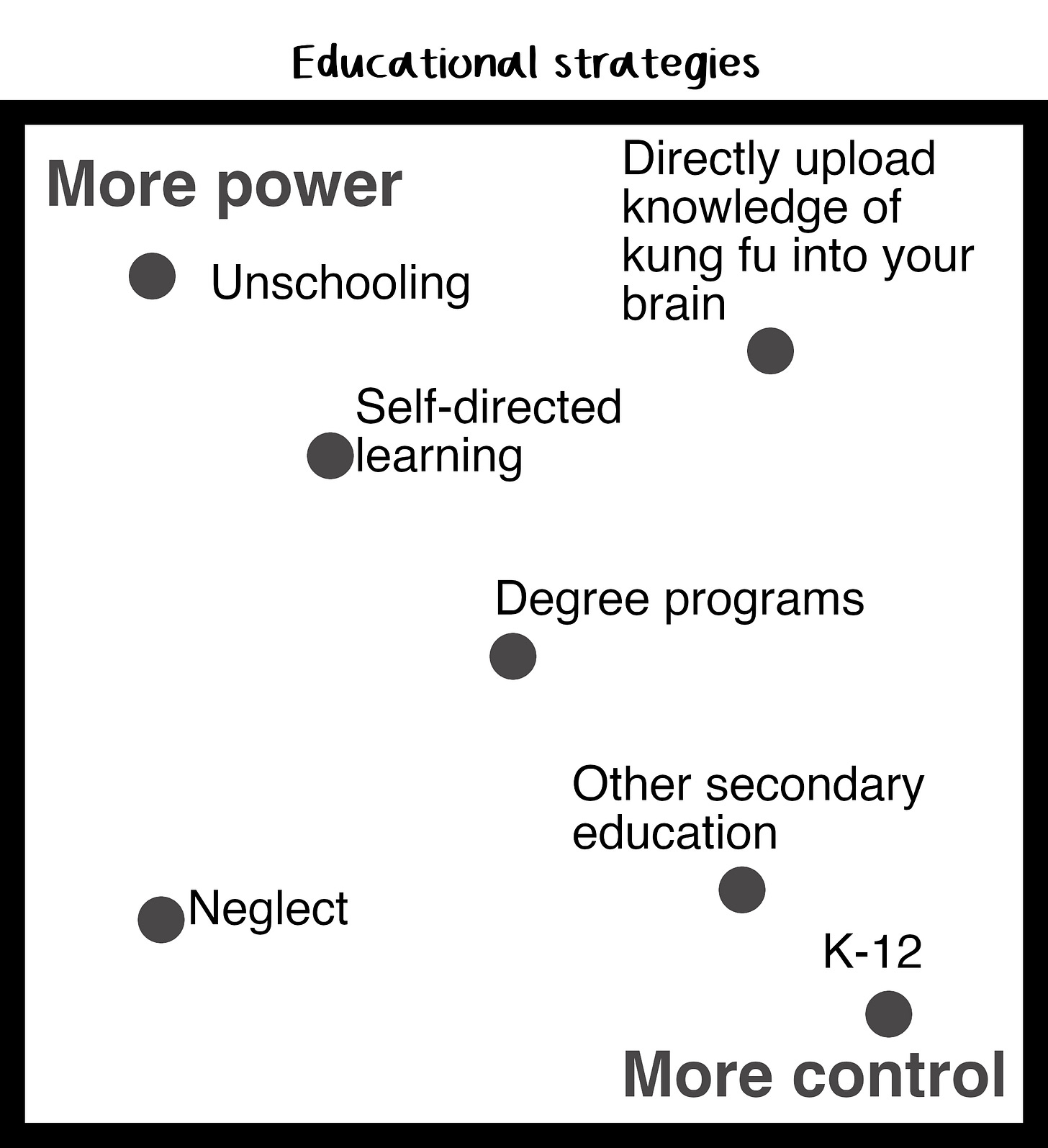
An example I’ve used before is that many states mandate that everybody learn a basic precursor to complex analysis before graduating high school. When society was deciding to put “identify zeros of polynomials, including complex zeros of quadratic polynomials” into the Common Core, we didn’t ask whether (trying) to learn this would be more worthwhile for the average student than taking an elective, or having a free period. We only really compared it to other math skills we could be mandating instead. If, some day, educators and legislators decide to make that optional, they won’t give students that time back. They’ll find something else to make mandatory.
Like, I hesitate to bring this up, but group theory, which the Common Core doesn’t mention at all, is in some sense more generally useful than complex analysis, and can be introduced at about the same difficulty level. According to my not-so-complex analysis technique of comparing the number of inbound links to their respective Wikipedia pages, there are 1,856 applications of group theory and only 1,377 applications of complex analysis. But it’s very obvious that identifying an abelian group is not an essential skill, seeing as how 99+% of people manage to go their entire lives without so much as reading the word “abelian.” Nothing bad happens if you don’t know it—it’s just something you might end up wanting to learn about if you’re studying certain aspects of theoretical physics, crystallography, control theory, art, or higher math. So I don’t think mandating it would be a good tradeoff.
In Creativity
When art feels complex, part of that richness is coming from the artist and part from their medium. The more control you surrender to your medium, the more complexity it’s allowed to contribute.2 There’s a lot of variation in how artists strike that balance.

The first two paintings, the Hofmann and Mønsted, each surrender a great deal of control. Hofmann lets his medium do a lot of the talking, while Mønsted’s realism gives the subject most of the authority. Van Gogh, with his precise but decidedly not realist brushwork, takes more control—neither the paint nor the forest can override what he’s expressing. The result is more personal and appealing, but it’s also, in a sense, smaller—a standard compression program would be able to compress the Van Gogh more efficiently than the Mønsted, and our eyes aren’t forced to linger on it like they are with the Hofmann.
I’ve been addicted for decades to creating images algorithmically. This is the one that got me hooked:
I “made” this in college, but I’m putting “made” in scare quotes because it’s so simple an algorithm, it’s more like I discovered it. Re-discovered it, really. Some readers will recognize it from having made it themselves, or having seen one somebody else made. Even in the more verbose programming languages, the formula for this pattern is usually only 3 characters long: x^y.
“Doodling” like that is addictive to me because of the instant gratification—I write a simple equation and immediately get something complex-looking. It’s creative power, but without much creative control. Here’s some output from an algorithm I made a couple weeks ago that fascinated my dad. (Sorry about the low resolution, Substack wouldn’t let me include a large gif).
Having done this for a while, I had an intuition about aspects of how it would look, but many details still surprised me, including how my visual cortex interpreted it differently at different stages of the animation. Here too, the algorithm for this is simple:
Take a photograph.
For each point in the photograph, measure its distance from the center, then move it that far up and that far left, wrapping around to the other side of the image if you go off the top or left edge.
In each animation frame, move each point diagonally towards its original position at a constant rate proportional to the distance, so that each point arrives at its original spot at the same time.
I chose “distance from the center” because when you do math with a 2D diagonal distance from a common center, you tend to get circles, and I like circles. I chose “that far up and to the left” because that’s easy to represent in a Cartesian coordinate system, and computers like Cartesian coordinate systems. Step 3 is just the easiest way to gradually undo the distortion. So I really had very little creative control here. (Also, in this case, it’s not even my own photograph.) Somebody else, plausibly, has done this exact thing.
This effect, in contrast, took me forever to code (well, a day, but that’s a long time for me to spend doing one thing). I kept futzing with it to get it to look exactly how it looked in my head. Finally getting there was satisfying, but overall I think I find this less satisfying than the last one. It’s partly a “you can’t tickle yourself” thing, but it’s also that I didn’t leave enough room for Ariel to mess around in.
This joyful play, incidentally, is what standardized math education tends to strangle in the crib.
In Macroeconomics
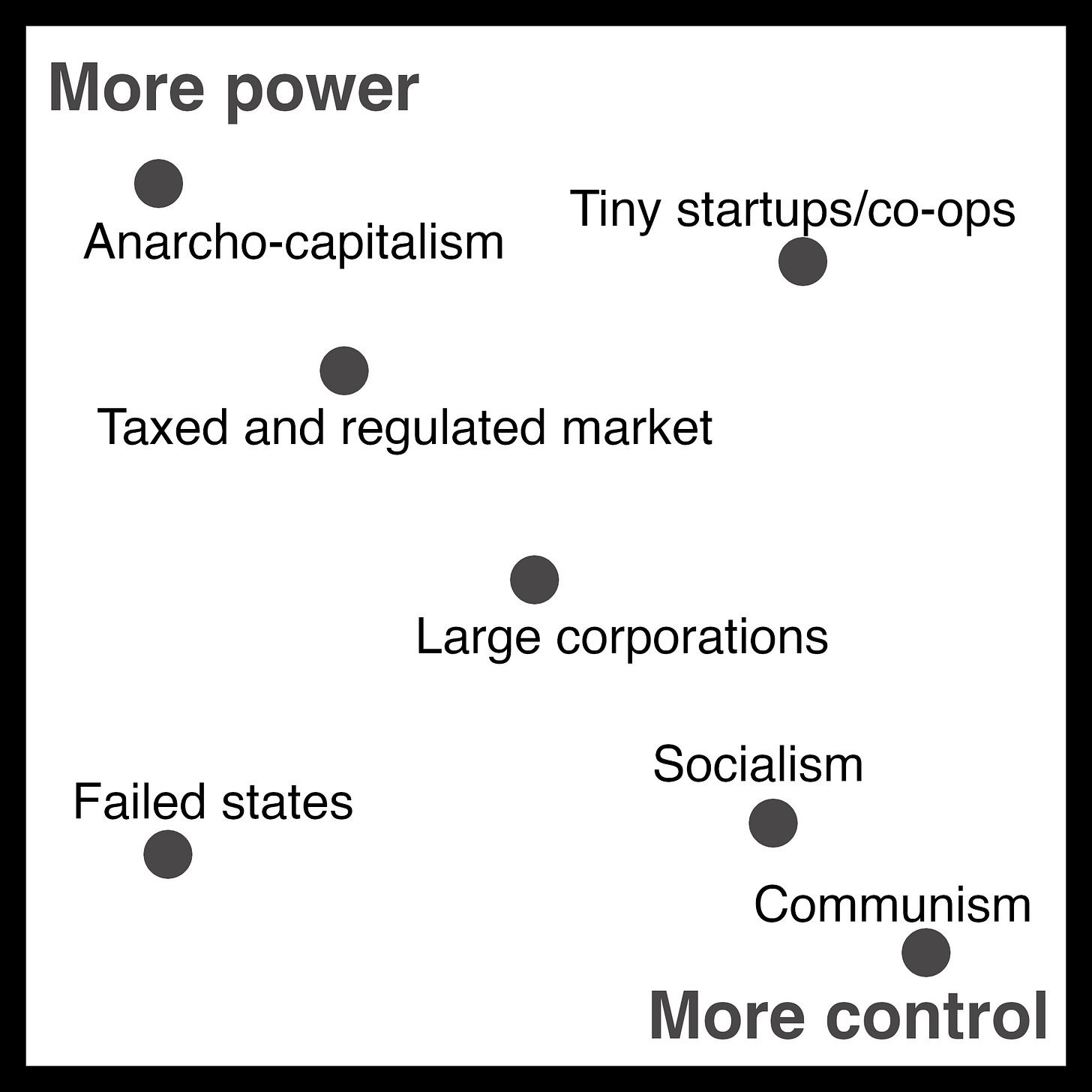
In centrally planned economies, everybody works together to build what the state’s decided they should build, which means less stuff ends up getting built because the state’s decision-making is a bottleneck. In free market economies, we build much more stuff, but a lot of that stuff is pointless or actively harmful, such as Las Vegas, most of the financial sector, or Facebook.
Every society makes this tradeoff fractally—or, well, it’s not infinitely deep, so more like the x^y image. A centrally planned economy is always partly dependent on “black markets” and usually also on international trade. A free market economy is dominated by corporations, which are almost universally run like Soviet states. In a corporation, resources are centrally allocated, goals are top-down, and it’s theoretically a meritocracy but in practice authority comes from seniority and how close you are to the founders. And when a corporation gets large enough, it starts to rely on internal black markets and financial incentives.
etc.
You get more, and hardier, plants if you don’t weed and let natural selection decide what grows. Even more powerful than a nail gun is hiring someone else to do all the work, as long as you’re okay with the possibility that they’ll nail the wrong thing to the wrong thing, or rob your house. Substack has more to offer than the Atlantic, but most of it is crap and some of it is Nazis.
There are many different ways to make this tradeoff.
In the human world, we tend to assume that the right or natural answer depends on physical scale—big powerful hammers, small precise hammers. But nature thinks differently—nuclear reactions are powerful, hard to control, and created by extremely small hammers. Paleontologists used to speculate that the larger dinosaurs had a secondary brain at the base of their tail, but they now seem fairly confident that no dinosaur was actually like that. It’s the smaller creatures, and the smaller organs, that sometimes need a little chaos in order to hum.
Further reading on this bit.